◄ Carnets Geol. 14 (9) ►
Contents
[1. Introduction] [2. Materials] [3.
Results]
[4. Discussion] [5. Conclusions] and ... [Bibliographic references]
Service de Géologie, Faculté Polytechnique, Université de Mons - UMONS, 20, Place du Parc, B-7000 Mons (Belgium)
Published online in final form (pdf) on June 19, 2014
[Editor: Bruno ;
language editor: Phil ]
Radiometric dating and astrochronologic dating still suffer discrepancies without knowing which one gives the most reliable results. A new tool is proposed to constrain both the approaches. The phase of the 405-kyr signal with respect to the Cretaceous - Paleogene boundary event has been determined in the Aïn Settara section (Kalaat Senan, central Tunisia). We use this phase value (Option 2), as well as an average of phase values obtained from the literature (Option 1), to examine the relationship linking both the radiometric (absolute) age assigned to the K-Pg boundary and the Cenozoic average-value of the ~405-kyr eccentricity period. A new useful constraint emerges: to any absolute age assumed for the K-Pg boundary corresponds a value of the mean Cenozoic 405-kyr period, and vice versa.
Supposing a K-Pg boundary radiometric age in the vicinity of 66.0 Ma, then the number of entire cycles (comprised between two minima of the 405-kyr eccentricity signal) within the Cenozoic Period could only be equal to 163. When adding to this figure the parts of the cycles preceding and following these 163 entire cycles the total duration of the Cenozoic Era becomes equal to 163.168 cycles (Option 1) or 163.081 cycles (Option 2).
We propose to grant a special interest to the determination of the 405-kyr cycle phase at stratigraphically well documented levels, particularly those that correspond to world-wide, sudden and catastrophic events, that are well located in time by reliable radiometric dates.
Cretaceous-Paleogene boundary; astrochronology; eccentricity; time scale.
M. (2014).- The Cretaceous-Paleogene boundary and its 405-kyr eccentricity cycle phase: a new constraint on radiometric dating and astrochronology.- Carnets de Géologie [Notebooks on Geology], Brest, vol. 14, nº 9, p. 173-189.
La limite Crétacé - Paléogène et la phase du cycle de 405 ka de l'excentricité : nouvelles contraintes sur la datation radiométrique et l'astrochronologie.- Les datations radiométriques et astrochronologiques ne s'accordent pas encore parfaitement, sans que l'on sache laquelle des deux approches est la plus précise. Un nouvel outil est proposé pour contraindre les résultats des deux méthodes. La position précise (phase) de la limite Crétacé - Paléogène (K-Pg) par rapport au cycle de 405 ka a été déterminée dans la coupe de l'Aïn Settara (Kalaat Senan, Tunisie centrale). Cette valeur de phase (Option 2), ainsi que la valeur moyenne des phases obtenues de la littérature (Option 1), sont utilisées pour étudier la relation qui lie l'âge radiométrique assigné à la limite K-Pg et la période moyenne, sur l'ensemble du Cénozoïque, du cycle de 405 ka. Il en résulte une contrainte intéressante : à chaque âge absolu assigné à la limite K-Pg correspond une valeur moyenne de la période du cycle de 405 ka et vice versa.
Si l'on suppose que l'âge radiométrique de la limite K-Pg se situe au voisinage de 66,0 Ma, alors, le nombre entier de cycles (compris entre deux minima du signal), que connaît le Cénozoïque, est de 163. Si on additionne à cette valeur la partie de cycle qui précède et celle qui suit ces 163 cycles entiers, on obtient une durée totale du Cénozoïque de 163,168 cycles (Option 1) ou de 163,081 cycles (Option 2).
Nous proposons de porter une attention particulière à la détermination de la phase du cycle de 405 ka par rapport aux horizons stratigraphiques les mieux connus, et particulièrement ceux qui correspondent à des événements soudains et catastrophiques, de portée mondiale, et qui sont bien datés radiométriquement.
Limite Crétacé-Paléogène ; astrochronologie ; excentricité ; échelle temporelle.
Catastrophism is the theory whereby the Earth was formerly affected by sudden, violent and short-duration events which had detrimental effects upon Life on the scale of the whole Planet. The end-Cretaceous mass extinction marked by an asteroid impact is the best well-studied example for that ( et al., 1980; & , 1980). On the Geological Time Scale development point of view, the most interesting characteristics of the K-Pg boundary are both its world-wide extension and its instantaneity, which makes this boundary a remarkable and outstanding time marker in the Geological Time Scale (, 1984; et al., 2008).
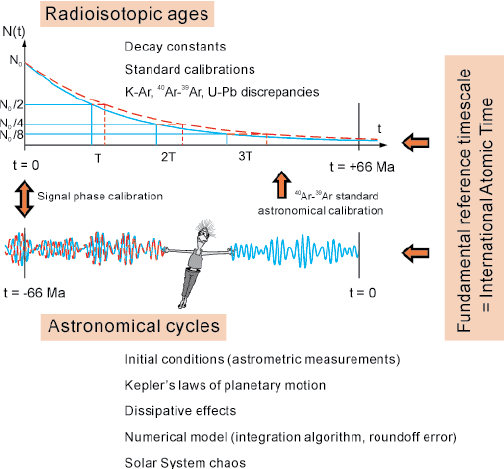
Click on thumbnail to enlarge the image.
Figure 1: Relationships between the radiometric and the astronomical chronometric scales. Signal phase calibration is the approach proposed in the present paper. Standard astronomical calibration is the dating of the 40Ar-39Ar standards using the astronomically derived scale ( et al., 2008; et al., 2011).
Figure 1 
shows the relationships between the radiometric and the astronomical chronometric scales. The figure shows that astronomers and geologists use very different methods for measuring stratigraphic time which constitute (theoretically) independent absolute dating methods, each one experiencing its own difficulties.
With recent advances in instrumentation and methodology, analytical uncertainties in radiometric dating have been pushed down to the range of 0.1 to 1% for both the 40Ar-39Ar and U-Pb dating systems. But progress must still be achieved in decay constants determination, standards calibration and K-Ar, 40Ar-39Ar and U-Pb reconciliation. Recently, et al. (2013) published a real breakthrough in the dating of the K-Pg boundary with a claimed uncertainty no more than 0.065 %.
Both radiometric and astronomical methods lead to inevitable discrepancies. It is very difficult to determine which one is the most accurate because error determination schemes apply to completely different scientific strategies. Although both of them seemed at first sight to be completely independent from each other, the geological time scale is more and more influenced by astronomical time scale. This is due to the following two reasons:
1) "tuning" of real geological data thanks to pre-calculated astronomical "target curves" ( et al.,
2004, 2011); in numerous studies, the geological record is constrained to a linear age to depth relationship based on the magnetic polarity time scale;
2) dating of the 40Ar-39Ar standards using the astronomically derived scale ( et al.,
2008; et al., 2011;
2012; 40Ar-39Ar standard astronomical calibration on
Figure 1 ).
The approach proposed in the present paper is referred to as a signal phase calibration in
Figure 1 .
Cyclic pelagic sedimentation such as alternations of marls and limestones mostly originate from astronomical forcing. In this case climatic variations influence the transfer of the detrital argillaceous fraction, coming from the platform top or the adjacent continental areas, and the carbonate sedimentation, which is constituted by benthic, pelagic, or winnowed platform top material. It was already shown that the lithological variations, induced by the variations of the Earth's orbit parameters in the band (periods from 20 to 400 kyr; , 1978a, 1978b; , 1988; & , 1991; et al., 2004, 2011) were appropriate to establish a very precise time scale (e.g., & , 1990; ten & , 1993; et al., 1993, 1999; & , 1995; , 1999; et al., 1999; , 1999; , 2000, 2005; et al., 2001; et al., 2003; & , 2003; et al., 2003; et al., 2005a, 2005b; et al., 2006; et al., 2006; et al., 2006; & , 2007; et al., 2007, 2008; et al., 2009; , 2012).
The orbital parameters, which influence terrestrial climates, are eccentricity, precession and obliquity. During geological times the precession and obliquity period lengths did not remain constant. Berger and his collaborators (e.g., et al., 1989a, 1989b; & , 1994) showed that the lengthening of the day and the lengthening of the Earth-Moon distance, as well as the reduction in the dynamic ellipticity of the Earth, during time, all induce a lengthening of the fundamental astronomical periods for precession and obliquity. For this reason it is essential to incorporate specific Earth parameters in the solution which affected the precession and obliquity frequencies. However, the exact values of these parameters have to come from the geological record (e.g., & , 2000) since they cannot be calculated directly from the astronomical solution itself ( et al., 2004, 2011). For this reason, together with the chaotic behaviour of the planetary motion in the solar system, precession and obliquity frequencies are difficult to constrain in a reliable manner in the distant past.
Nevertheless, the entire Neogene has been astronomically tuned, resulting in a standard Geological Time Scale of unprecedented accuracy and resolution ( et al., 2005a). An astronomically calibrated deep-sea record of the entire Oligocene was recently performed ( et al., 2006). Tuning efforts for the earlier parts of the Paleogene are also in progress ( et al., 2003; et al., 2005b; et al., 2007, 2008). The extension of this tuning to older time intervals critically depends on the accuracy of astronomical solutions that are used to calculate the astronomical target curves.
In spite of the proven chaotic behaviour of the solar system, eccentricity periods are known to be very stable in time and have not probably significantly varied during the last 100 Ma (, 1989, 1999; et al., 2003; et al., 2004, 2011). The very stable 405-kyr eccentricity component is assumed to be adequate to tune the entire Cenozoic and Mesozoic timescale ( et al., 2004). This 405-kyr cycle is particularly important to establish a precise cyclostratigraphic based scale: firstly because of its greater stability compared to the other cycles (, 1999; et al., 2004), secondly because its length is closer to the time scales usually used by geologists (biozones, magnetozones) and thus is more easily correlated with that scales. Some authors already showed the interest of this 405-kyr cycle for Upper Cretaceous and Paleocene stratigraphy (, 1999; et al., 1999; et al., 2005b; et al., 2007, 2008; et al., 2008; et al., 2011; , 2012; et al., 2012).
The rotational frequency of the major axis (secular frequency) of a planet is usually indicated by "g" plus an index identifying the planet position relative to the Sun. For example, g2 and g5 are the secular frequencies of respectively Venus and Jupiter and are expressed in arcsec yr-1. The period P is obtained from the frequency thanks to the formula: P (yr) = 1 296 000/ν (arcsec yr-1). If g5 secular frequency is equal to 4.25745 arcsec yr-1 ( et al., 2004, Table 4), then Pg5 period is 304 408 yr. If g2 secular frequency is equal to 7.4574 arcsec yr-1, then Pg2 period equals 173 787 yr.
The secular frequency responsible for the ~405-kyr eccentricity cycle is the beat g2-g5.
If, e.g., g2-g5 = 7.45740 - 4.25745 = 3.19995 arcsec yr-1, then Pg2-g5 = 405 006 yr.
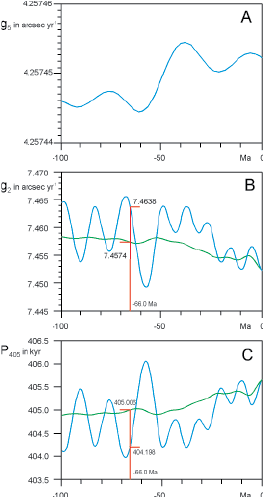
Click on thumbnail to enlarge the image.
Figure 2:
Variation of the secular frequencies g5 (Jupiter) and g2 (Venus) from -100 Ma to 0 Ma (present-day) and the resulting P405 period of eccentricity.
A. Secular frequency of Jupiter g5 in arcsec yr-1 (from et al.,
2004,
Fig. 9).
B. Secular frequency of Venus g2 in arcsec yr-1 (from et al.,
2004,
Fig. 9). For an arbitrary age of 66.0 Ma, the instantaneous value of g2 = 7.4638 arcsec yr-1 (blue line) and the [-66.0; 0] time interval average of g2 = 7.4574 arcsec yr-1 (green line).
C. P405 period of eccentricity in kyr recalculated from A and B. For the arbitrary age of 66.0 Ma, the instantaneous value of P405 = 404.198 kyr (blue line) and the [-66.0; 0] time interval average of P405 = 405.006 kyr (green line). A constant g5 = 4.25745 arcsec yr-1 have been chosen for the calculation.
The variation of the secular frequencies of Jupiter (g5) in the time interval from -100 Ma to 0 Ma is shown in
Figure 2.A
(data from et al., 2004, Fig. 9). Figure
2.B
gives (in blue) the secular frequency of Venus g2 in arcsec yr-1 and (in green) the cumulative average departing from present-day. For an arbitrary age of 66.0 Ma the figure shows an instantaneous value of g2 = 7.4638 arcsec yr-1 and an average value of g2 = 7.4574 arcsec yr-1 in the [-66.0; 0] time interval.
Note that in the [-100; 0] interval g5 varies by about 0.0000105 arcsec yr-1 and g2 varies by about 0.0163 arcsec yr-1. Assuming a constant g5 = 4.25745 arcsec yr-1 for calculation,
Figure 2.C
shows the resulting P405 period of eccentricity (in kyr). For the arbitrary age of 66.0 Ma, the instantaneous value of P405 = 404.198 kyr and the [-66.0; 0] time interval average of P405 = 405.006 kyr.
In the nineties, the K-Pg boundary was generally given a value of 65.0 Ma ( et al., 1992, 1993; et al., 1993; et al., 1994; & , 1995; et al., 1995; & , 1996).
In a magnetostratigraphic and geochronologic study of the Hell Creek and basal Fort Union formations of south-western North Dakota, et al. (2002) proposed an age of 65.51 ± 0.1 Ma. The Geologic Time Scale GTS2004 ( et al., 2005) gave a radiometric age of 65.5 ± 0.3 Ma.
Eccentricity cycles have been used in an attempt to date the K-Pg and other important Paleogene boundaries and events. The main problem with the astronomical age model is that different tuning options to the 405-kyr eccentricity cycle exist for the older part of the Paleogene. It results that the number and tuning of 405-kyr cycles remain undecided ( et al., 2008; et al., 2010; et al., 2011; et al., 2012).
et al. (2003) proposed, in an interesting astronomical calibration of the Early Paleocene of the Zumaia section in the Basque region of Spain, a K-Pg boundary age of 65.83 Ma. See also discussion in et al. (2013).
et al. (2008, Table 1), in a valuable astronomical calibration of the entire Paleocene period, proposed three options for the K-Pg boundary age, respectively: ~65.28, ~65.68 and ~66.08 Ma. They believed the second figure corresponds to the best estimate.
Joining radiometric and astronomical dating et al. (2008) give new (astronomical) calibrations of 28.201 ± 0.046 Ma for the Fish Canyon sanidine standard. The authors then recalculated the K-Pg boundary age values proposed by et al. (1992, 1993) and et al. (1991). The new figures are:
et al. (1992, 1993): 65.81 ± 0.14 Ma (melt rock of Chicxulub crater), 65.84 ± 0.12 Ma (sanidine of Z coal), 65.99 ± 0.12 Ma (sanidine of IrZ coal), 65.84 ± 0.16 Ma (Haitian tektites);
et al. (1991): 65.98 ± 0.10 Ma (Haitian tektites).
Thus according to et al. (2008) the radiometric age of the K-Pg boundary ranges from 65.8 to 66.0 Ma and is probably close to ~65.95 Ma. et al. (2010) gave ages of ~66.0 and ~56.0 Ma for the K-Pg and P-E boundaries.
The approach consisting in the astronomical calibration of Ar-Ar standards has been continued by et al. (2011). The astronomically calibrated 40Ar/39Ar age for Fish Canyon sanidine standard gives now 28.172 ± 0.028 Ma (0.10 %).
et al. (2011) presented combined radiometric dating (U-Pb zircon) and cyclostratigraphic analysis of the carbon isotope excursion at the Paleocene-Eocene boundary in Spitsbergen, constraining on the numerical age of the Paleocene-Eocene boundary. Incorporating the total uncertainty from both radiometric and cyclostratigraphic datasets gives an age ranging from 55.728-55.964 Ma. Combined with the assumption that the Paleocene Epoch spans twenty-five 405 kyr cycles, their new age for the boundary suggests an age of ~66 Ma for the K-Pg boundary.
et al. (2012) developed an intercalibrated astrochronologic and radiometric time scale for the Cenomanian-Turonian boundary interval near the Global Stratotype Section and Point in Colorado (Western Interior Basin, USA). They obtained a Cenomanian-Turonian boundary age of 1) 93.89 ± 0.14 Ma or 2) 93.90 ± 0.15 Ma. With an estimated duration between the Cenomanian-Turonian and the Cretaceous-Paleogene boundaries of 27.94 ± 0.16 Ma, it results an age of about 65.95 or 65.96 Ma for the Cretaceous-Paleogene boundary.
et al. (2012a) give for the K-Pg boundary an age of 65.95 ± 0.05 Ma and et al. (2012b) an age of 65.91 ± 0.11 Ma. et al. (2012c) indicate that the new Geologic Time Scale 2012 sets the K-Pg boundary at 66.0 Ma. In this volume set, et al. (2012, Table 28.4) give a figure of 65.95 ± 0.05 Ma following both a "radio-isotopic model" and an "astronomical model", the "combined age model = final GTS2012 version" corresponding then to 66.04 ± 0.05 Ma.
et al. (2012) put forward a possible error in the cyclostratigraphical interpretation of the sections used by et al. (2011) in determining their 40Ar-39Ar age for the Fish Canyon sanidine neutron fluence monitor. The new interpretation leads to an age of 27.89 Ma for the Fish Canyon sanidine. This new interpretation is highly controversial since it gives an age of 65.250 ± 0.06 Ma for the K-Pg boundary.
et al. (2013) performed 40Ar/39Ar dating on sanidine separated from four bentonites in three distinct coal beds within two geographically distant stratigraphic sections in the Hell Creek region of northeastern Montana. Extensive studies in this region have documented faunal, floral, and chemostratigraphic aspects of latest Cretaceous through early Paleogene terrestrial strata. Both sections contain well-documented Ir anomalies coincident with the biostratigraphically defined K-Pg boundary. In the Hauso Flats section, they analyzed samples from two localities ~200 m apart of a bentonite from the IrZ coal, located stratigraphically only a few centimeters above the horizon yielding the largest iridium anomaly reported from this area and 5 cm above the highest occurrence of Cretaceous pollen in the section. All of the data combined yield a weighted mean age of 66.043 ± 0.043Ma. In the same Hauso Flats section, the authors have used both the 40Ar/39Ar dating on sanidine and the U-Pb dating on zircon to obtain very comparable results. et al. (2013) also analyzed multiple samples of the tektites from Beloc, Haiti, obviously linked to the Chicxulub impact, to test for synchrony of the K-Pg boundary with the impact. Obtained data yields an age of 66.038 ± 0.049 Ma for the tektites. Both ages are indistinguishable from each other with a much reduced uncertainty of 32 kyr and suggest that the Chicxulub impact event coincides with the K-Pg boundary. Dating of et al. seems to be a real breakthrough in the dating of this particular reference mark.
In the sections where the 405-kyr eccentricity cycling is known to encompass the Cretaceous - Paleogene boundary event (e.g., the Aïn Settara section, Kalaat Senan, central Tunisia) we determine the phase of the 405-kyr signal with respect to this boundary level. We could use the phase value to examine the relationship linking both the radiometric (absolute) age assigned to the K-Pg boundary and the Cenozoic average-value of the ~405-kyr eccentricity period. To any absolute age assumed for the K-Pg boundary there corresponds a value of the mean Cenozoic 405-kyr period, and vice versa.
Supposing a K-Pg boundary radiometric age in the vicinity of 66.0 Ma, then the number of entire cycles (comprised between two minima of the 405-kyr eccentricity signal) within the Cenozoic Period could only be equal to a certain figure. When this figure is added to the parts of the cycles preceding and following these entire cycles, the total duration of the Cenozoic Era can be determined as a precise decimal number of cycles.
Published data that allow the precise determination of the ~405-kyr signal phase with respect to the K-Pg boundary event have been collected from literature. Five studies have been selected: 1) the et al. (1999) and (1999) study of South Atlantic Deep Sea Drilling holes, 2) the et al. (2008) study of South Atlantic Deep Sea Drilling holes and Zumaia coastal section, 3) the et al. (2011) study of ODP Holes, 4) the et al. (2012) study of the upper Maastrichtian of the Zumaia section, and 5) the (2012) study of the Tunisian Aïn Settara section.
et al. (1999) and (1999) studied Upper Cretaceous Deep Sea Drilling cores from the South Atlantic. Sites included two drill holes from the Rio Grande Rise off the coast of Brazil (Holes 357, 516F) and four from the Walvis Ridge (Holes 525A, 527, 528 and 529). Good core recoveries, favourable sedimentation rate, rarity of turbidite deposition and/or slumping, and good magnetostratigraphic and biostratigraphic data make the region ideal for reliable cyclostratigraphic study. Sediments recovered displays alternations of bright white calcareous layers and greyish green more clayey intervals. Calibration of reflectance to measure carbonate content showed the utility of the reflectance data to study the climato-astronomical cyclicity. This work disclosed cycles showing the full hierarchy of eccentricity amplitude modulations that would be expected of precessional orbital forcing. The ~100-kyr and 405-kyr cycles were particularly useful for time measuring and for hole-to-hole core correlations.
Three cores (516F, 528 and 525A) have been used here to give the 405-kyr cycle position with respect to the K-Pg boundary, the C29r/C30n boundary and the Micula prinsii first occurrences (FO) positions ( et al., 1999, Fig. 9; , 1999, Fig. 6).
et al. (2008) provided the first study of a complete cyclic sedimentary succession for the early Paleogene from multiple holes that have been drilled during two ODP expeditions: Leg 198 (Shasky Rise, NW Pacific Ocean) and Leg 208 (Walvis Ridge, SE Atlantic Ocean). High resolution X-ray fluorescence (XRF) core scanner and other non-destructive core logging data from Sites 1209 through 1211 (Leg 198) and Sites 1262, 1267 (Leg 208) were performed.
These new records allowed the authors to build a comprehensive astronomically calibrated stratigraphic framework with unprecedented accuracy for both the Atlantic and the Pacific Oceans, covering the entire Paleocene epoch, based on the identification by Gaussian filtering of the 405-kyr eccentricity cycle. The land-based Zumaia section (Basque Basin, northern Spain) has been integrated as well.
et al. (2008) used high-resolution XRF Fe intensity data for the deep sea cores and the amount of terrigenous material for Zumaia (100 - Carbonate wt. %; ten & , 1993). We have chosen here the well documented results from Walvis Ridge Sites 1262 and 1267, and Zumaia.
et al. (2011) recovered the 405-ka orbital eccentricity variation in the well preserved Maastrichtian sedimentary series from ODP (Ocean Drilling Program) Holes 1258A (Leg 207, Equatorial Atlantic), 1267B (Leg 208, South Atlantic), 762C (Leg 122, Indian Ocean) and DSDP (Deep Sea Drilling Program) Hole 525A (Leg 74, South Atlantic). Cyclostratigraphic analysis was performed on high resolution measurements of magnetic susceptibility on sediments cored during Legs 207 and 208, and gray level variations of sediment color obtained from core photographs from Legs 122 and 74. Identification of the astronomical cycles leads to the definition of a detailed cyclostratigraphic frame from the upper Campanian to the Cretaceous-Paleogene boundary.
By comparison to the most recent astronomical solution La2010a ( et al., 2011), the authors proposed two different ages for the K-Pg boundary, considering the uncertainty of the long-term variation of the 405 ka eccentricity cycle. The first proposal provides a K-Pg boundary age of 65.59 ± 0.07 Ma and the second an age of 66.00 ± 0.07 Ma.
et al. (2012) studied the upper Maastrichtian of the Zumaia section in the Basque country (northern Spain) that contains a cyclic alternation of limestones and marls deposited in a hemipelagic setting. In this section, the stacking pattern of the lithologies shows a hierarchy that reflects the combined influence of the orbital parameters of precession and eccentricity. This is confirmed by time series analyses of lithological and geochemical data (magnetic susceptibility MS, reflectance L* and stable carbon isotope δ13C), indicating a strong influence of eccentricity-modulated precession on the latest Cretaceous climate.
In a previous paper (, 2012), a new approach to highlight the presence of the 405-kyr cycle in the marl-limestone alternation of the Aïn Settara section (central Tunisia) was presented, with the final aim of determining the cycle phase with respect to the Cretaceous-Paleogene boundary event (= K-Pg boundary or KPB in formulas). The principal relevant results of this publication were the following:
The Aïn Settara section exposes a continuous and well preserved section of marl-limestone alternation, including the upper part of the Maastrichtian and the basal Danian ( et al., 2001; & , 2003).
This succession revealed the superposition of several modes of alternations, corresponding to the combined orbito-climatic signal of eccentricity and precession. The ~100-kyr eccentricity cycle and the ~21-kyr precession cycle allowed the construction of a floating chronometric scale. The possible presence of an obliquity signal of minor importance is taken into account in the analysis ( & , 2003).
In addition to the description of the ~100-kyr eccentricity and the ~21-kyr precession cycles, precession cycle-duration modulation permitted the highlighting of the ~405-kyr eccentricity cycle (, 2012).
The recognition of the very stable ~405-kyr eccentricity cycle permitted confirmation of the relevance of the previously established chronometric scale. Particularly, it especially allowed determination of the ~405-kyr signal phase with respect to the K-Pg boundary event: the 405-kyr cycle minima values are -363 kyr and +42 kyr, relative to the K-Pg boundary. A correction for the variations of the ~100-kyr cycle duration gave the minima positions of -373 kyr and +32 kyr (, 2012).
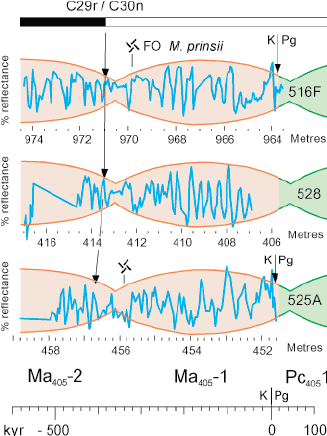
Click on thumbnail to enlarge the image.
Figure 3: Recognition of the 405-kyr cycles to the K-Pg boundary vicinity in three deep sea sediment cores (from et al., 1999, Fig. 9, and , 1999, Fig. 6; modified). The green parts of the envelope curves correspond to the 405-kyr cycle added by symmetry. The notation of the of 405-kyr cycles (e.g., Ma405-1) comes from et al. (2008).
The results of et al.
(1999, Fig. 9) and
(1999,
Fig. 6) are shown in Figure 3 . The data of (and collaborators) are obtained from drill sites by the Deep Sea Drilling Project in the South Atlantic. Information is stratigraphically constrained using: magnetostratigraphy, the K-Pg boundary location and the Micula prinsii FO location. The 405-kyr cycle is given on the basis of the amplitude variations in the reflectance signal.
According to Figure 3 , the minimum of the 405-kyr eccentricity the nearest to the K-Pg boundary falls about 30 kyr after the boundary for 516F and 36 kyr after the boundary for 525A. Unfortunately, it should not be forgotten that et al.
(1999,
Fig. 9) and (1999, Fig. 6) do not give the exact position of the minima of the 405-kyr cycle that follows the K-Pg boundary. This position was obtained by symmetry departing from their figure (green parts of the envelope curves corresponding to our own drawing).
Another difficulty that can arise is the question of the completeness of the deep sea drilling sections. Deep-sea sections have often been shown to contain major hiatuses. & (1991a, 1991b) demonstrated that K-Pg boundary hiatuses spanning from 60 to 500 kyr are present in nearly all deep-sea sections deposited at depths below 1000 m. A marine transgression shifted the locus of sedimentation to continental shelf areas, leading to sediment starvation and non-deposition and/or erosion in the deep-sea ( & , 1991a, 1991b; et al., 1993; , 1995). They concluded that most deep-sea sites exhibit K-Pg boundary hiatuses whereas outer neritic to upper bathyal settings (El Kef, Caravaca, Agost) are stratigraphically more complete across the boundary, although hiatuses could occur later in the Danian.
Other cases of deep sea drilling K-Pg boundary discontinuities are quoted, e.g.: the ODP Hole 750A in the southern Indian Ocean ( et al., 1992) and the DSDP Site 384 in NW Atlantic Ocean ( et al., 2000, p. 28-31). On the contrary, certain oceanic sections provided the K-Pg boundary Ir anomaly and other characteristic objects, reinforcing the idea of sedimentary continuity through the boundary, e.g.: the LL44-GPC3 core in the Pacific ( & , 1986; et al., 1987; et al., 1993) and the Demerara Rise ODP Leg 207 in western North Atlantic ( et al., 2007).
Concerning Site 516F, (1983) considered the section to be continuous across the K-T boundary. He described the boundary (p. 757) as "major changes in benthic faunal composition at the Cretaceous/Tertiary boundary transition. It was a time of rapid turnover, with the extinctions of numerous species and the introduction of many new species". Nowadays, if "the extinctions of numerous species" suggests a catastrophic event, "the introduction of many new species" in the nearby overlying level is rather indicative of an hiatus.
Concerning Site 525A, & (1998) said that the K-Pg boundary corresponds to the first appearance of the Danian species Parvularogoglobigerina eugubina, wich marks Zone P1a. This suggests that the K-Pg boundary transition at Site 525A is very condensed and a short hiatus may be present. Following & (2003), the Maastrichtian of site 525A would be complete. According to & (1991a, 1991b), 50-200 kyr of basal Danian might be missing at Sites 525, but & (1992) and & (1993) disagreed. & (1993) believed that non-recognition of Zone P0 at some deep-sea sites is due to very low sedimentation rates and the temporally short interval represented by Zone P0.
The preceding discussion reveals that the deep sea sediment cores are often more difficult to interpret than the onshore sections.
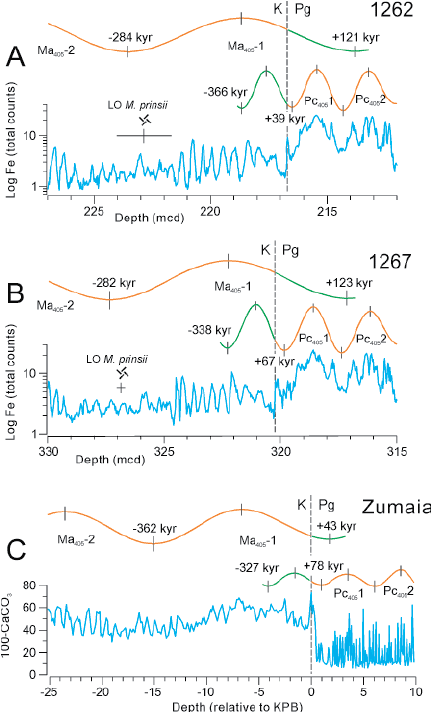
Click on thumbnail to enlarge the image.
Figure 4: Recognition of the 405-kyr cycles to the K-Pg boundary vicinity in (A) toceanic hole Site 1262, (B) oceanic hole Site 1267 (Leg 208) and (C) the coastal cliff at Zumaia (all three modified from et al., 2008, Fig. 4). In our figure the signals expressing the 405-kyr cyclicity (orange lines) were extrapolated (green lines) beyond the K-Pg boundary as if the latter did not correspond to a change in sedimentation rate. The position of the K-Pg boundary between the two minima gives the phase.
Figure 4
represents a modified part of the Fig. 4 from et al.
(2008). It shows the cyclostratigraphic interpretation of the sedimentary succession encompassing the K-Pg boundary for sediments from Walvis Ridge (Sites 1262 and 1267, Leg 208) and Zumaia (Basque Basin, northern Spain). The long eccentricity related cycle has been extracted by Gaussian filtering ( et al.,
2008). These 405-kyr cyclicity signals (orange lines), considered separately for Maastrichtian sediments and for Danian sediments, were here extrapolated (green lines) beyond the K-Pg boundary as if the latter did not correspond to an abrupt change in sedimentation rate. Considering an arbitrary cycle duration of 405 kyr, the minima ages with respect to the K-Pg boundary have been indicated for both the Maastrichtian and the Danian curves.
This relatively simplistic graphical treatment seems to highlight a sedimentary gap at the K-Pg boundary for Sites 1262 and 1267. On the contrary, in the Zumaia section the approach gives an "extra time" recording.
& (2012) used the impact-induced Os isotope excursion at the K-Pg boundary as a test for the completeness of the earliest Danian sequences. In ODP 1262B the Os isotope excursion is closely associated with the biostratigraphically defined K-Pg boundary, and a gradual recovery to pre-impact 187Os/188Os ratios is observed. These features are interpreted by the authors as evidence of a complete K-Pg boundary section. On the contrary, at ODP 1209C the excursion occurs approximately 10 cm below the biostratigraphic K-Pg boundary and the gradual recovery to pre-impact 187Os/188Os ratios is absent. According to & (2012), this K-Pg boundary section is probably not complete.
et al. (2003) performed an interesting cyclostratigraphic study of the Danian and the lower part of the Selandian stages in the Zumaia section (Basque basin, northern Spain). Unfortunately, it cannot be used as comparison material in the present work:
The K-Pg boundary by itself has not constituted a target of this Zumaia study, which investigates strictly the Paleocene part of the section.
et al. (2003) admitted that eccentricity modulations of precession cycles at the 405-kyr period were not unambiguously detected. On the contrary, et al. (2008) and et al. (2008) maintained that the 405-kyr cyclicity is quite discernible in the section.
At Zumaia, the first 2 m above the K-Pg boundary seem to be problematic. The first, abnormally thick, ~100-kyr eccentricity cycle, as interpreted by et al. (2003), could in fact represent two cycles ( et al., 2008).
et al. (2013) performed a cyclostratigraphic study of the Upper Maastrichtian succession in the Zumaia section. This very recent work should be included in a future study on the position of the K-Pg boundary within the 405-kyr eccentricity cycle.
et al. (2011, Fig. 5) proposed two options for the astronomical calibration of the Maastrichtian. Both the options are based on the 405-kyr eccentricity variations extracted from the sedimentary record of Sites 762C, 1258A and 525A by filtering, compared to the 405-ka variations extracted from the astronomical solution La 2010a. The proposed options are offset by one 405-ka eccentricity cycle. Following their figure, if we fix the K-Pg boundary at an arbitrary time of 0 kyr and the duration of the cycle at 405 kyr, then the last Cretaceous minima is situated at -338 kyr and the first Paleogene minima is situated at +67 kyr.
et al. (2012) studied the upper Maastrichtian of the Zumaia section. In this work, the expression of the 405-kyr eccentricity cycle present in the section served as a primary signal for astronomical tuning, i.e., use of a constant duration of 405 kyr between eccentricity minima and linear interpolation between these points. In their Fig. 6, the magnetic susceptibility (MS), reflectance (L*) and stable carbon isotope (δ13C) data series, in the time domain, were treated by band-pass filters to extract the 405-kyr signal. That signal is used here to locate the phase with respect to the K-Pg boundary corresponding to each lithological and geochemical data set. For the magnetic susceptibility, reflectance and stable carbon isotope data series, the last Cretaceous minima is situated, respectively, at circa -382 kyr, -367 kyr, -308 kyr, and the first Paleogene minima is situated, respectively, at circa +23 kyr, +38 kyr, +97 kyr.
Determination of the 405-kyr signal phase with respect to the K-Pg boundary event in the Aïn Settara section based on (2012, Table 2) results in 405-kyr cycle minima values at -363 kyr and +42 kyr relative to the K-Pg boundary (indicated as "raw data" within , 2012, Table 2). A correction for the variations of the ~100-kyr cycle duration gave the minima values of -373 kyr and +32 kyr (indicated as "corrected data"). Only the corrected data are used in the present paper.
| Reference | Locality | This work | Min. before K-Pg (kyr) | Min. after K-Pg (kyr) |
| et al., 1999, Fig. 9 | 516F, 525A |
Fig. 3 |
-362 | 43 |
| et al., 2008, Fig. 4 | 1262 | Fig. 4.A
Cretaceous |
-284 | 121 |
| Fig. 4.A
Paleogene |
-366 | 39 | ||
| 1267 | Fig. 4.B
Cretaceous |
-282 | 123 | |
| Fig. 4.B
Paleogene |
-338 | 67 | ||
| Zumaia | Fig. 4.C
Cretaceous |
-362 | 43 | |
| Fig. 4.C
Paleogene |
-327 | 78 | ||
| et al., 2011, Fig. 5 | 1267B | -338 | 67 | |
| et al., 2012, Fig. 6 | Zumaia - delta 13C | -308 | 97 | |
| Zumaia - L* | -367 | 38 | ||
| Zumaia - MS | -382 | 23 | ||
| Option 1 (average) | -337.82 | 67.18 | ||
| (standard deviation) | 32.73 | 32.73 | ||
| , 2012, Fig.
14 |
Aïn Settara (corrected) | Option 2 | -373 | 32 |
Table 1: Recapitulation the available data concerning the K-Pg boundary position (phase) compared to the 405-kyr eccentricity cycle (defined on its minima).
Table 1 recapitulates the available data concerning the K-Pg boundary position (phase) compared to the 405-kyr eccentricity cycle (defined on minima). Looking at the part of the 405-kyr eccentricity cycle following the K-Pg boundary, it results that two different options could be taken into account:
Option 1
The value corresponds to the average of 11 values coming from the literature. It equals to 67.18 ± 65.46 kyr (2 s.d.).
Option 2
The value corresponds to the only 32 ± 6 kyr value of (2012), considered here as the more accurate available figure.
The Option 1 value comes mainly from the average of data not designed for determining the phase of the 405-kyr eccentricity cycle with respect to the K-Pg boundary, but for sequences encompassing a larger stratigraphic interval. They are thus relatively inaccurate and imprecise at the needed time interval level. On the contrary, Option 2 was especially designed for that purpose (, 2012) on a rather short, well exposed, onshore section.
The 405-kyr cyclicity makes it possible to build a floating scale around the K-Pg boundary. This floating scale can be used as a correlation tool. It can also be used for precise determination of the durations of stratigraphic intervals (i.e., biozones, magnetozones, etc.). Moreover, the recognised stability of the 405-kyr cycle encourages trying to obtain a present-day anchored cyclicity time-scale.
An important question relates to the number of 405-kyr cycles that exist between the K-Pg boundary (KPB) and the present-day (PD).
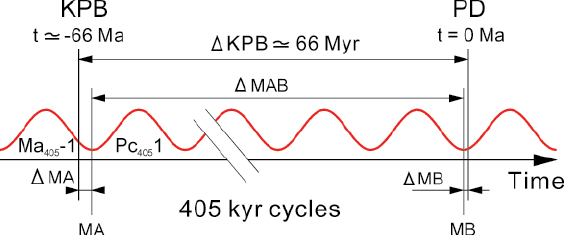
Figure 5
illustrates the problem.
Δ KPB = duration separating KPB from PD
MA = cycle minimum that directly follows the KPB
Δ MA = duration separating MA from the KPB
MB = cycle minimum that directly precedes PD
Δ MB = duration separating MB from PD
Δ MAB = duration corresponding to the number of entire 405-kyr cycles (NEC) comprised between the KPB and PD.
Click on thumbnail to enlarge the image.
Figure 5: Determination of the number of 405-kyr cycles existing between K-Pg boundary (KPB) and present-day (PD).
MA = cycle minimum that directly follows the KPB
Δ MA = duration separating MA from the KPB
MB = cycle minimum that directly precedes PD
Δ MB = duration separating MB from PD
Δ MAB = duration corresponding to the number of entire 405-kyr cycles (NEC) comprised between the KPB and
PD
Δ KPB = K-Pg boundary absolute age
Value of Δ MA
The determination of the part of the 405-kyr eccentricity cycle following the K-Pg boundary (Δ MA) was the subject of preceding paragraphs. It resulted that two options could be taken into account (Table 1):
Option 1: The Δ MA value corresponds to the average of the 11 values coming from the literature. It equals to 67.18 ± 65.46 kyr (2 s.d.).
Option 2: The Δ MA value corresponds to the only 32 ± 6 kyr value of (2012).
Value of Δ MB
et al. (2004) gave a simple formula furnishing the value of the 405-kyr cycle eccentricity. The minima of the 405-kyr cycle preceding present-day time (=MB) is situated at -760 yr. The value of Δ MB is thus 0.76 kyr.
Determination of Δ MAB
Figure 5
shows that: Δ MAB = Δ KPB - Δ MA - Δ MB. If the K-Pg boundary (KPB) is placed, e.g., at -66.0 Ma, and Δ MA equals 32 kyr (Option 2), then one has between MA and MB (the two minima of the 405-kyr cycle):
Δ MAB = 66000 - 32 - 0.76 = 65967.24 kyr. ± 6 kyr
Click on thumbnail to enlarge the image.
Figure 6: Relation linking the Cenozoic average period of the 405-kyr cycle to the absolute age assigned to the K-Pg boundary. NEC = number of entire cycles. See text for details.
As Δ MAB depends at the same time on both the exact period P405 (kyr) and the number of entire cycles (NEC) comprised between MA and MB, we can deduce the relations that can exist between P405 and Δ MAB, or, what is more useful, between the absolute age assigned to the KPB and P405.
Figure 6
shows this last relation.
The linear equations giving the possible relations are:
P405 (kyr) = (Δ KPB - Δ MB - Δ MA) / NEC
Option 1:
If Δ MA = 67.18 kyr then P405 (kyr) = (Δ KPB - 67.96) / NEC = Δ KPB/NEC - 67.96/NEC
Option 2:
If Δ MA = 32 kyr then P405 (kyr) = (Δ KPB - 32.76) / NEC = Δ KPB/NEC - 32.76/NEC
We can now fix the NEC.
Option 1:
If NEC = 161, then P405 (kyr) = 0.0062111 * Δ KPB - 0.42211
If NEC = 162, then P405 (kyr) = 0.0061728 * Δ KPB - 0.41951
If NEC = 163, then P405 (kyr) = 0.006135 * Δ KPB - 0.41693
If NEC = 164, then P405 (kyr) = 0.0060975 * Δ KPB - 0.41439
Option 2:
If NEC = 161, then P405 (kyr) = 0.0062111 * Δ KPB - 0.203478
If NEC = 162, then P405 (kyr) = 0.0061728 * Δ KPB - 0.202022
If NEC = 163, then P405 (kyr) = 0.006135 * Δ KPB - 0.200982
If NEC = 164, then P405 (kyr) = 0.0060975 * Δ KPB - 0.199756
These straight-line equations associate then the couples formed by
1) the age assigned to the K-Pg boundary and 2) the period of the 405-kyr cycle that correspond to the signal phase for diverse NEC figures. They show what ages can be assumed for the K-Pg boundary for the most recently published P405 durations ( et al.,
2004, 2011). Conversely, if we could know with a high degree of accuracy the K-Pg boundary age, then
Figure 6
gives the most suitable averaged P405 duration along the entire Cenozoic Era. The figure, of course, indicates also the most probable value for NEC, which is equal to 163.
Click on thumbnail to enlarge the image.
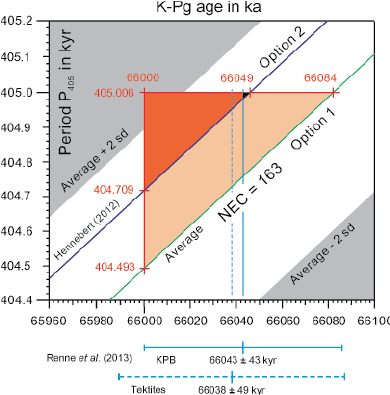
Figure 7: Detail of the relation linking the Cenozoic average period of the 405-kyr cycle to the absolute age assigned to the K-Pg boundary. See text for details.
Figure 7
gives a close-up view on the relation that links the absolute age assigned to the K-Pg boundary and the Cenozoic average period of the 405-kyr cycle (P405). The equations above give, for a NEC = 163 and a Δ KPB = 66000 kyr, a P405 = 404.493 kyr (Option 1) or a P405 = 404.709 kyr (Option 2).
If we fix NEC at 163 and P405 at 405.006 kyr (see
Fig. 2 ), then the K-Pg age is 66.084 Ma (Option 1) or 66.049 Ma (Option 2).
Option 1:
Δ KPB (ka) = 163 * P405 (kyr) + 67.96
If P405 = 405.006 kyr, then Δ KPB = 66084 kyr
Option 2:
Δ KPB (ka) = 163 * P405 (kyr) + 32.76
If P405 = 405.006 kyr, then Δ KPB = 66049 kyr
Remember that the NEC figure corresponds only to the number of entire cycles defined as existing between two minima of the 405-kyr eccentricity signal.
The total number of cycles within the entire Cenozoic can also be calculated. The part of the cycle preceding the present-day (Δ MB) equals 0.76 kyr. The part of the cycle following the K-Pg boundary (Δ MA) equals to 67.18 ± 65.46 kyr (2 s.d.; Option 1) if we take into account the average of the data coming from the literature, or only the 32 kyr value if we consider the (2012) figure (Option 2).
Option 1:
The sum of both the partial cycles is then: Δ MA + Δ MB = 67.18 + 0.76 = 67.94 kyr.
These 67.94 kyr correspond to 67.94/405 cycle, i.e., 0.168 cycle. Then the first option gives 163.168 cycles for the entire Cenozoic Era.
Option 2:
The sum of both the partial cycles is now: Δ MA + Δ MB = 32 + 0.76 = 32.76 kyr.
These 32.76 kyr correspond to 32.76/405 cycle, i.e., 0.081 cycle. Thus the second option gives 163.081 cycles for the entire Cenozoic Era.
Values calculated above for Option 1 and 2 were obtained without any hypothesis on the exact duration of the "405-kyr cycle" or on the exact K-Pg boundary age. One must recall that the parts of "405-kyr cycle" (Δ MA and Δ MB) were arbitrarily fixed to a cycle of exactly 405 kyr, but that actually in the beginning they were expressed as relative quantities. This is why one can affirm that there was no influence of this arbitrary choice on the final result, except for the "164th" cycle precisely fixed at 405 kyr.
According to Figure 1 , one could suppose that it is possible to reach the same result following two completely different ways. Unfortunately, the matter is not so simple. Radiometric dating of a given sample or level furnishes a unique date (with a certain precision and accuracy). On the contrary, astronomical models furnish a repetitive signal and it is usually difficult to specify how many cycles separate two observed events. This problem is recurrent when determinating the "astronomical age" of the K-Pg boundary event. Until recently, one do not knew how many 405-kyr cycles separate this event from the Present Day and thus it was not possible to specify an astronomically-based age ( et al.,
2008; et al.,
2010; et al.,
2011; et al.,
2012).
Recent results of et al. (2013) permit to chose an astronomically-based option of ~66.08 Ma for the K-Pg boundary event (,
2013).
Moreover, another (more philosophical) problem appears. Due to the (supposed?) superiority of the astronomical timescale versus the radioisotopic timescale, the latter is increasingly dependent on astronomical models regarded as ideal to define a "geological standard time" or Astronomical Time Scale (ATS; , 1982; et al., 1990; , 1991; et al., 1994; et al., 1995; , 1999; et al., 1999; & , 2007).
Radiometric error is thought to be linearly linked to time. On the contrary, astronomical error increases dramatically with time due mainly to chaos and dissipative effects (see: & ,
2007,
Fig. 2.E). For recent dates (less than 20 Ma), astronomical error is close to the best accuracy that one can hope with radiometric dating (~0.1%). It is the reason why 40Ar-39Ar standards have been dated using the astronomical scale ( et al.,
2008; et al., 2011; et al.,
2012; see: 40Ar-39Ar standard astronomical calibration in
Fig. 1 , this publication). et al.
(2008) compared astronomical and 40Ar-39Ar ages of tephras in marine deposits in Morocco to calibrate the age of Fish Canyon sanidine, the most widely used standard in 40Ar/39Ar geochronology. This calibration resulted in a more precise age of 28.201 ± 0.046 Ma and reduced the
absolute uncertainty of 40Ar/39Ar method from ~2.5 to 0.25%. et al.
(2011) reported a new high-precision 40Ar-39Ar age for the Fish Canyon sanidine (FCs) neutron fluence monitor of 28.172 ± 0.028 Ma. The authors also improved the concordance between 40Ar-39Ar and U-Pb dating techniques such that dates of unprecedented reliability are now possible for all the Phanerozoic.
et al. (2012) suggested a possible error in the cyclostratigraphical interpretation of the sections used by the preceding authors, leading to a new age of 27.89 Ma for the Fish Canyon sanidine. This new interpretation is highly controversial since it gives an age of 65.250 ± 0.06 Ma for the K-Pg boundary. The very recent K-Pg boundary dating by et al. (2013) clearly contradict recent work of et al.
The 40Ar-39Ar standard astronomical calibration, as valuable that it is, presents a hidden philosophical problem. It clearly illustrates the fact that the radiometric scale is increasingly dependent on the astronomical models regarded as defining our "standard time".
The new approach presented in this work represents an attempt to confront radiometric dating vs. astronomical cycles, treating both equally as long as possible. The approach could be named: signal phase calibration (see
Fig. 1 ). Its aim is to furnish an additional constraint to radiometric and astronomical dating. To achieve this end, it is necessary to improve:
1) the K-Pg boundary radiometric dating itself, 2) the astronomical solutions, and
3) the 405-kyr cycle phase at the K-Pg boundary. The first two are currently carried out:
the radiometric ages become increasingly precise and reliable ( et al., 2010; et al., 2011; et al., 2012b; et al., 2012; et al., 2013);
the astronomical solutions are also improved ( et al., 2004, 2011).
The third target (3) necessitates a special effort on the best K-Pg sections offering a good astronomical signal in an environment of fast and continuous sedimentation. The work at the Aïn Settara section (,
2012) reveals that this could be achieved on relatively short (onshore) sections. The final hope is to see in the near future the convergence of all three aspects of the problem, that is to say obtaining a significant reduction in the size of the uncertainty triangle in
Figure 7 . The same approach will be also followed on other boundaries,
e.g., the Paleocene-Eocene and the Eocene-Oligocene boundaries.
1. Based on (2012), the recognition of the very stable ~405-kyr eccentricity cycle in the Aïn Settara Cretaceous-Paleogene boundary section allowed determination of the ~405-kyr signal phase with respect to the K-Pg boundary event. A correction for the variations of the ~100-kyr cycle duration gave -373 kyr and +32 kyr respectively, which was used in the present paper for signal phase calibration (Option 2). The consideration of several signal phases coming from the literature gave, in contrast to the +32 kyr figure, an average of +67.18 kyr with a standard deviation of 32.73 kyr (Option 1).
2. The value of the phase of the 405-kyr signal with respect to the K-Pg boundary event is used to examine the relation linking the radiometric (absolute) age assigned to the K-Pg boundary and the average value of the ~405-kyr cycle period. It results in a useful new constraint: to any absolute age assumed for the K-Pg boundary there corresponds a precise and accurate value of the average Cenozoic 405-kyr period, and vice versa.
3. Supposing a K-Pg boundary (radiometric) age equal or close to 66.0 Ma, the number of entire cycles within the Cenozoic Period could only be 163. By definition, one entire cycle is comprised between two minima of the 405-kyr eccentricity. Adding the parts of the cycles preceding and following these 163 entire cycles, one obtains a total duration of the Cenozoic of 163.168 cycles (Option 1) or 163.081 cycles (Option 2).
4. For better accuracy, it is necessary to improve still the K-Pg boundary radiometric dating, the astronomical solution and the 405-kyr cycle phase. Meanwhile, this paper concludes that there already exists a very good fit between the most recent and precise et al. (2013) dating of the K-Pg boundary, the period P405 determined as the average for the entire Cenozoic era ( et al., 2004), and the Option 2 correlation-line coming from the (2012) data.
5. In conclusion, we propose to devote special interest to the determination of the ~405-kyr cycle phase with respect to stratigraphically well documented levels and particularly those that correspond to sudden and catastrophic events, and that are well located in time by reliable radiometric dates.
Francis and Christian (University of Mons) are thanked for many profitable discussions on Tunisian geology and constructive comments on an earlier version of the manuscript. I am also grateful to Michael (University of Vienna), Jaume (Instituto Nazionale di Geophysica e Vulcanologia, Rome) and to an anonymous reviewer for their helpful comments. I am very grateful to the Language Editor, Phil , for his corrections which allowed significant improvements to the manuscript. I greatly thank also the Editor Bruno for his hard work and his patience with me.
S. & G. (2003).- Planktonic foraminiferal response to the latest Maastrichtian abrupt warm event: a case study from South Atlantic DSDP Site 525A.- Marine Micropaleontology, Amsterdam, vol. 48, p. 225-249.
L.W., W., F. & H.V. (1980).- Extraterrestrial cause for the Cretaceous-Tertiary extinction.- Science, Washington, vol. 208, p. 1095-1108.
F.C., L.D., E., X., N.J. & Y. (1994).- The astronomical theory of climate and the age of the Brunhes-Matuyama magnetic reversal.- Earth and Planetary Science Letters, La Jolla, vol. 126, nº 1-3, p. 91-108.
S.J., M., A.S., F.J., S., J., D., F., X., N., J. (2012).- Cyclostratigraphy and astronomical tuning of the Late Maastrichtian at Zumaia (Basque country, Northern Spain).- Earth and Planetary Science Letters, La Jolla, vol. 359-360, p. 264-278.
A.L. (1978a).- Long-term variations of caloric insolation resulting from the Earth's orbital elements.- Quaternary Research, Amsterdam, vol. 9, p. 139-167.
A.L. (1978b).- Long-term variations of daily insolations and Quaternary climatic changes.- Journal of Atmospheric Sciences, Boston, vol. 35, nº 12, p. 2362-2367.
A. & M.F. (1991).- Insolation values for the climate of the last 10 million years.- Quaternary Science Reviews, Amsterdam, vol. 10, p. 297-317.
A. & M.F. (1994).- Astronomical forcing through geological time. In: P.L. de & D.G. (eds.), Orbital forcing and cyclic sequences.- Special Publications of the International Association of Sedimentologists, Oxford, vol. 19, p. 15-24.
A., M.F. & V. (1989a).- Influence of the changing lunar orbit on the astronomical frequencies of Pre-Quaternary insolation patterns.- Paleoceanography, Washington, vol. 4, nº 5, p. 555-564.
A., M.F. & V. (1989b).- Pre-Quaternary frequencies.- Nature, London, vol. 342, nº 6246, p. 133.
W.A., D.V., C.C. & M.-P. (1995).- A revised cenozoic geochronology and chronostratigraphy. In: W.A., D.V., M.-P. & J. (eds.), Geochronology, time scales and global stratigraphic correlation.- Society of Economic Paleontologists and Mineralogists, Special Publication, Tulsa, vol. 54, p. 129-212.
W.A., M.-P., M., D.V., R.D. & F. (2000).- Integrated Paleocene calcareous plankton magnetobiochronology and stable isotope stratigraphy: DSDP Site 384 (NW Atlantic Ocean).- Palæogeography, Palæoclimatology, Palæoecology, Amsterdam, vol. 159, p. 1-51.
W.B.N. (1984).- The Cretaceous-Tertiary boundary - The ideal geologic time scale boundary?- Newsletters on Stratigraphy, Stuttgart, vol. 13, nº 3, p. 143-155.
B.F., P.J. & E.E. (1987).- Schocked quartz in the Cretaceous-Tertiary boundary clays: Evidence for a global distribution.- Science, Washington, vol. 236, p. 705-709.
S.C. & D.V. (1995).- Revised calibration of the geomagnetic polarity timescale for the Late Cretaceous and Cenozoic.- Journal of Geophysical Research, Washington, vol. 100, p. 6093-6095.
A.J., D.J., I.C., H., J.E.A., Y., L. & I.W. (2011).- Constraints on the numerical age of the Paleocene/Eocene boundary.- Geochemistry, Geophysics, Geosystems, Washington, vol. 12, nº 6, Q0AA17, 19 p. (doi:10.1029/2010GC003426).
S.C. (1999).- An astronomical tuning strategy for Pliocene sections: implications for global-scale correlation and phase relationships.- Philosophical Transactions of the Royal Society, London, vol. A 357, p. 1949-1973.
S. & T.D. (1992).- Comment on "Hiatus distributions and mass extinctions at the Cretaceous/Tertiary boundary".- Geology, Boulder, vol. 20, nº 4, p. 380-381.
D.H. (1983).- Late Cretaceous and Paleocene benthic foraminifers from Deep Sea Drilling Project Site 516, Rio Grande Rise, western South Atlantic.- Initial Reports of the Deep Sea Drilling Project, College Station, TX (Ocean Drilling Program), vol. 72, p. 757-782.
G.B., G.A., L.W. & J.D. (1993).- 40Ar/39Ar age spectra and total-fusion ages of tektites from Cretaceous-Tertiary boundary sedimentary rocks in the Beloc Formation, Haiti.- U.S. Geological Survey Bulletin, Washington, nº 2065, 20 p.
J., J.I., V., X., G. & S. (2003).- Untangling the Palaeocene climatic rhythm: an astronomically calibrated Early Palaeocene magnetostratigraphy and biostratigraphy at Zumaia (Basque basin, northern Spain).- Earth and Planetary Science Letters, La Jolla, vol. 216, nº 4, p. 483-500.
J., V., K. & J. (2013).- Detailed correlation and astronomical forcing within the Upper Maastrichtian succession in the Basque Basin.- Boletín Geológico y Minero, Madrid, vol. 124, nº 2, p. 253-282.
C., E., E., R., N.P., I., J.A., F., M., E., R. & I. (2001).- The Cretaceous-Palaeogene (K/P) boundary in the Aïn Settara section (Kalaat Senan, Central Tunisia): lithological, micropalaeontological and geochemical evidence.- Bulletin de l'Institut royal des Sciences naturelles de Belgique, Sciences de la Terre, Bruxelles, vol. 71, p. 169-190.
N., X., O., L.G. & P.Y. (2006).- Lower Cretaceous stage durations combining radiometric data and orbital chronology: Towards a more stable relative time scale?- Earth and Planetary Science Letters, La Jolla, vol. 246, p. 407-417.
S., M., R, A. & R. (2003).- Orbitally modulated black shale deposition in the upper Albian Amadeus Segment (central Italy): a multi-proxy reconstruction.- Palæogeography, Palæoclimatology, Palæoecology, Amsterdam, vol. 190, p. 441-458.
F.M. & J.G. (1996).- A Phanerozoic timescale.- Episodes, Beijing, vol. 19, nº 1-2, p. 5-9 (1 chart).
F.M., F.P., J.G., J., P. van, J. & Z. (1994).- A Mezozoic time scale.- Journal of Geophysical Research, Washington, vol. 99, p. 24051-24074.
F.M., J.G. & A. (eds., 2005).- A Geologic Time Scale 2004.- Cambridge University Press, Cambridge, 384 p.
F.M., J.G. & F.J. (2012a).- On the Geologic Time Scale.- Newsletters on Stratigraphy, Stuttgart, vol. 45, nº 2, p. 171-188.
F.M., J., G. & M. (coord., 2012b).- Improving the Geologic Time Scale. In: High fidelity: the quest for precision in stratigraphy and its applications (16-17 May 2012, London).- The Geological Society, London, p. 36-37.
F.M., J.G., M. & G. (eds., 2012c).- The Geologic Time Scale 2012 2-Volume Set.- Elsevier, Amsterdam, 1176 p.
M. (2012).- Hunting for the 405-kyr eccentricity cycle phase at the Cretaceous-Paleogene boundary in the Aïn Settara section (Kalaat Senan, central Tunisia).- Carnets de Géologie [Notebooks on Geology], Brest, Article 2012/05 (CG2012_A05), p. 93-116.
M. & C. (2003).- Proposition d'une échelle chronométrique autour de la limite Crétacé-Paléogène par cyclostratigraphie : coupe de l'Aïn Settara (Kalaat Senan, Tunisie centrale).- Géobios, Villeurbanne, vol. 36, p. 707-718.
M., F. & S. (2009).- Cyclostratigraphy and chronometric scale in the Campanian - Lower Maastrichtian: the Abiod Formation at Ellès, central Tunisia.- Cretaceous Research, London, vol. 30, p. 325-338.
T.D. (1999).- Toward a composite orbital chronology for the Late Cretaceous and Early Palaeocene GPTS.- Philosophical Transactions of the Royal Society, London, vol. A 357, p. 1735-1759.
T.D. & S.L. (1990).- Precessional climate cyclicity in Late Cretaceous-Early Tertiary marine sediments: a high resolution chronometer of Cretaceous-Tertiary boundary events.- Earth and Planetary Science Letters, La Jolla, vol. 99, p. 263-275.
T.D., J. & S. (1999).- Precessional cycles in Upper Cretaceous pelagic sediments of the South Atlantic: Long-term patterns from high-frequency climate variations. In: E. & C.C. (eds.), Evolution of the Cretaceous ocean-climate system.- Geological Society of America, Special Paper, Boulder, vol. 332, p. 105-120.
J.F., K.R., J.D., L. & D. (2002).- Magnetostratigraphy and geochronology of the Hell Creek and basal Fort Union formations of southwestern North Dakota and a recalibration of the age of the Cretaceous-Tertiary boundary. In: J.H., K.R. & D.J. (eds.), The Hell Creek Formation and the Cretaceous-Tertiary boundary in the northern Great Plains: An integrated continental record of the end of the Cretaceous.- Geological Society of America, Special Paper, Boulder, vol. 361, p. 35-55.
F.J. (1991).- Astronomical calibration of Gauss to Matuyama sapropels in the Mediterranean and implication for the Geomagnetic Polarity TimeScale.- Earth and Planetary Science Letters, La Jolla, vol. 104, Issues 2-4, p. 226-244.
F.J. (2008).- Recent progress in the standardization and calibration of the Cenozoic Time Scale.- Newsletters on Stratigraphy, Stuttgart, vol. 43, nº 1, p. 15-22.
F.J., L.J., A. & M.F. (1993).- Evaluation of the astronomically calibrated time scale for the latest Pliocene and earliest Pleistocene.- Paleoceanography, Washington, vol. 8, nº 5, p. 549-565.
F.J., W., C.G., L.J., A. & W.J. (1995).- Extending the astronomical (polarity) timescale into the Miocene.- Earth and Planetary Science Letters, La Jolla, vol. 136, nº 3-4, p. 495-510.
F.J., H., W., C.G., L.J., J.E., I., J., E., N., J.R. & W.J. (1999).- Present status of the astronomical (polarity) time-scale for the Mediterranean Late Neogene.- Philosophical Transactions of the Royal Society, London, vol. A 357, nº 1757, p. 1931-1947.
F.J., K.F. & L.J. (2010).- Evaluation of the astronomical time scale for the Paleocene and earliest Eocene.- Earth and Planetary Science Letters, La Jolla, vol. 300, nº 1-2, p. 139-151.
L.A. (2000).- New perspectives on orbitally forced stratigraphy.- Annual Reviews of Earth and Planetary Science, Palo Alto, vol. 28, p. 419-475.
L.A. (2005).- Earth's orbital parameters and cycle stratigraphy. In: F.M., J.G. & A. (eds.), A Geologic Time Scale 2004.- Cambridge University Press, Cambridge, p. 55-62.
L.A. & J.G. (2007).- Cyclostratigraphy and the Astronomical Time scale.- Stratigraphy, New York, vol. 4, nº 2-3, p. 239-251.
M.R. & A.S. (eds., 1995).- Orbital forcing timescales and cyclostratigraphy.- Geological Society Special Publications, London, nº 85, 210 p.
D., B., J., L.A., N., S. & R.E. (2011).- Astronomical calibration of the Maastrichtian (Late Cretaceous).- Earth and Planetary Science Letters, La Jolla, vol. 305, nº 3-4, p. 328-340.
G.A., G.B. & L.W. (1991).- 40Ar/39Ar age of Cretaceous-Tertiary boundary tektites from Haiti.- Science, Washington, vol. 252, p. 1539-1542.
R.G. (1982).- Brunhes-Matuyama magnetic reversal dated at 790,000 yr B.P. by marine-astronomical correlations.- Quaternary Research, vol. 17, nº 2, p. 135-147.
W.G.H.Z. ten & A. (1993).- Orbital cyclicities above and below the Cretaceous/Paleogene boundary at Zumaya (N Spain), Agost and Relleu (SE Spain).- Sedimentary Geology, Amsterdam, vol. 87, nº 1-2, p. 69-101.
G., N., J.B. & C.B. (1993).- Is there evidence for Cretaceous/Tertiary boundary-age deep-water deposits in the Caribbean and Gulf of Mexico?- Geology, Boulder, vol. 21, p. 776-780.
K.F., A., F.J., W., P.R. & J.R. (2008).- Synchronizing Rock Clocks of Earth History.- Science, Washington, vol. 320, nº 5875, p. 500-504.
F.T., M., G.R. & L. (1993).- Cenozoic sedimentation history of the central North Pacific: Inferences from the elemental geochemistry of core LL44-GPC3.- Geochimica et Cosmochimica Acta, Amsterdam, vol. 57, nº 8, p. 1719-1740.
F.T. & J.T. (1986).- Accretion rate of extraterrestrial matter: Iridium deposited 33 to 67 million years ago.- Science, Washington, vol. 232, p. 1225-1229.
J. (1988).- Secular evolution of the solar system over 10 million years.- Astronomy and Astrophysics, Paris, vol. 198, p. 341-362.
J. (1989).- A numerical experiment on the chaotic behaviour of the Solar System.- Nature, London, vol. 338, p. 237-238.
J. (1999).- The limits of Earth orbital calculations for geological time-scale use.- Philosophical Transactions of the Royal Society, London, vol. A 357, nº 1757, p. 1735-1759.
J., P., F., M., A.C.M. & B. (2004).- A long term numerical solution for the insolation quantities of Earth.- Astronomy & Astrophysics, vol. 428, nº 1, p. 261-285.
J., A., M. & H. (2011).- La2010: A new orbital solution for the long term motion of the Earth.- Astronomy & Astrophysics, Paris, vol. 532, paper A89, 15 p.
L. & G. (1998).- Maastrichtian climate, productivity and faunal turnovers in planktic foraminifera in South Atlantic DSDP sites 525A and 21.- Marine Micropaleontology, Amsterdam, vol. 33, p. 55-86.
L.J., F.J., J., N.J. & D. (2005a).- The Neogene Period. In: F.M., J.G. & A.G. (eds.), A Geologic Time Scale 2004.- Cambridge University Press, p. 409-440.
L.J., A., D., J. C., E., U., J. & I. (2005b).- Astronomical pacing of late Paleocene to early Eocene global events.- Nature, London, vol. 435, p. 1083-1087.
K.G., D.L., B.T. & C. (2007).- Impact and extinction in remarkably complete Cretaceous-Tertiary boundary sections from Demerara Rise, tropical western North Atlantic.- Geological Society of America Bulletin, Boulder, vol. 119, nº 1-2, p. 101-115.
N. (1995).- Graphic correlation of high latitude Cretaceous-Tertiary boundary sequences at Nye Kløv (Denmark), ODP Site 690 (Weddell Sea), and ODP Site 738 (Kerguelen Plateau): Comparison with the El Kef (Tunisia) boundary stratotype.- Modern Geology, London, vol. 19, p. 109-147.
N. & G. (1991a).- Hiatus distribution and mass extinctions at the Cretaceous/Tertiary boundary.- Geology, Boulder, vol. 19, nº 5, p. 497-501.
N. & G. (1991b).- How complete are Cretaceous/ Tertiary sections? A chronostratigraphic estimate based on graphic correlation.- Geological Society of America Bulletin, Boulder, vol. 103, p. 1439-1457.
S.R., S.E., B.S., B.B., D.J., J.D., B.R. & D.A. (2012).- Intercalibration of radioisotopic and astrochronologic time scales for the Cenomanian-Turonian boundary interval, Western Interior Basin, USA.- Geology, Boulder, vol. 40, nº 1, p. 7-10.
R.K. & C. (1993).- Controversies on the placement of the Cretaceous/Tertiary boundary and the K/P mass extinction of planktonic foraminifera.- Palaios, Tulsa, vol. 8, p. 127-139.
H. (2013).- Impact and extinction.- Science, Washington, vol. 339, p. 655-656.
H. & N.J. (2000).- Constraints on astronomical parameters from the geological record for the last 25 Myr.- Earth and Planetary Science Letters, La Jolla, vol. 182, p. 1-14.
H., N.J. & U. (2001).- Astronomical forcing in Late Eocene marine sediments.- Earth and Planetary Science Letters, La Jolla, vol. 193, p. 589-602.
H., R.D., J.O., P.A., H.K., C.H., N.J., A.K. & B.S. (2006).- The heartbeat of the Oligocene climate system.- Science, Washington, vol. 314, p. 1894-1898.
G. & D. (2012).- A geochemical clock in earliest Paleogene pelagic carbonates based on the impact-induced Os isotope excursion at the Cretaceous-Paleogene boundary.- Paleoceanography, Washington, vol. 27, PA3219, doi:10.1029/2012PA002301.
P.R., A.L., F.J., K.F., D.F., W.S., L.E., R. & J. (2013).- Time scales of critical events around the Cretaceous-Paleogene Boundary.- Science, Washington, vol. 339, nº 6120, p. 684-687.
T., M., C., F.J. & K. (2011).- A refined astronomically calibrated 40Ar/39Ar age for Fish Canyon sanidine.- Earth and Planetary Science Letters, La Jolla, vol. 311, p. 420-426.
N.J., A. & W.R. (1990).- An alternative astronomical calibration of the lower Pleistocene timescale based on ODP site 677.- Transactions of the Royal Society of Edinburgh, vol. 81, p. 251-261.
N.J., I.N. & G.P. (1999).- Astronomical () calibration of the geological time-scale.- Philosophical Transaction of the Royal Society, London, vol. A 357, p. 1731-2007.
J. & J. (1980).- An extraterrestrial event at the Cretaceous-Tertiary boundary.- Nature, London, vol. 285, p. 198-200.
M., R., F., N. & F. (2006).- Orbital tuning of a lower Cretaceous composite record (Maiolica Formation - Central Italy).- Paleoceanography, Washington, vol. 21, PA4212, doi: 10.1029/2005PA001224.
C.C., J.M., A., S.V., P., W., P., E., F.J.M.R., G.H., J. & M.O. (1992).- Coeval 40Ar/39Ar ages of 65.0 million years ago from Chicxulub Crater melt rock and Cretaceous-Tertiary boundary tektites.- Science, Washington, vol. 257, nº 5072, p. 954-958.
C.C., L. & R.F. (1993).- 40Ar/39Ar dating and magnetostratigraphic correlation of the terrestrial Cretaceous-Paleogene boundary and Puercan Mammal age, Hell Creek-Tullock formations, eastern Montana.- Canadian Journal of Earth Sciences, Ottawa, vol. 30, p. 1981-1996.
N., F.J. & R.P. (2012).- The Paleogene Period. In: F.M., J.G., M.D. & G.M. (eds.), The Geologic Time Scale 2012.- Elsevier, Boston, Volume 2, Chapter 28, p. 855-921.
F., B. & M. (2003).- Successive refinements in long-term integrations of planetary orbits.- The Astrophysical Journal, Washington, vol. 592, p. 620-630.
M., J. & S. (2012).- Nannofossil biostratigraphy, strontium and carbon isotope stratigraphy, cyclostratigraphy and an astronomically calibrated duration of the Late Campanian Radotruncana calcarata Zone.- Cretaceous Research, London, vol. 38, p. 80-96.
T., U., J., I., J., L.J. & J.C. (2007).- On the duration of magnetochrons C24r and C25n and the timing of early Eocene global warming events: Implications from the Ocean Drilling Program Leg 208 Walvis Ridge depth transect.- Paleoceanography, Washington, vol. 22, nº 2), PA2201, doi: 10.1029/2006PA001322.
T., U., I., E., S., V., J. & H.F. (2008).- Astronomical calibration of the Paleocene time.- Palæogeography, Palæoclimatology, Palæoecology, Amsterdam, vol. 257, p. 377-403.
T., U. & J. (2012).- Time scale controversy: Accurate orbital calibration of the early Paleogene.- Geochemistry, Geophysics, Geosystems, Washington, 13, Q06015, 19 p., doi: 10.1029/2012GC004096.
J.C., M.-P., W.A., T., F. & K.C. (1992).- Chemobiostratigraphy of the Cretaceous/Paleocene boundary at Site 750, Southern Kerguelen Plateau. In: Jr S.W., R., A.A., M.-P., W.A., P.R., N.A., J., M.F., D.M., F., M.A., R., W.R., H., K., D.B., A., T., M., E., P.Q., F., V.J.M., J.H., M., A., D.K., H., J. & R. (partipating scientists), Central Kerguelen Plateau.- Proceedings of the Ocean Drilling Program, Scientific Results, College Station, TX (Ocean Drilling Program), vol. 120, chapter 54, p. 961-977.